Guest Post by
Sergio Cantu, Pedro Lopes, QuEra Computing Inc.
Quantum computing’s potential hinges on its ability to perform reliable, complex, and extensive computations. However, qubits are very fragile objects where environmental noise and imperfect control will invariably hinder the performance of quantum computers. This makes the pursuit of quantum error correction paramount.
Quantum error correction is a formidable challenge. To date, no at-scale demonstration of error-corrected quantum algorithms has been realized. The complexity of qubit control for error correction operations varies depending on the quantum computing platform selected. In this context, neutral atoms emerge as a compelling choice for qubits due to their excellent isolation from the environment, which minimizes decoherence, and the inherent reproducibility of atomic qubits. Moreover, atoms offer a low-overhead interface for control with exceptional precision, using lasers and magnetic fields to handle internal energy levels where qubits and information are coded.

In this article, we shed some light on a less-explored but remarkable feature offered by neutral-atom architectures for error correction: the ability to operate “transversal gates” with ease. Much of the perspective below was revealed by Dolev Bluvstein from Harvard University in a talk in June this year at the Frontiers of Interacting Systems of Rydberg Atoms II workshop.
To appreciate this topic’s relevance, one must first grasp the nature of quantum error correction’s information encoding and manipulation. For our present purpose, it is necessary to understand that error correction utilizes the redundancy of multiple noisy qubits to encode the logical information of a perfect qubit. It simulates a nearly flawless qubit by collectively working on a cluster, or patch, of these noisy qubits.
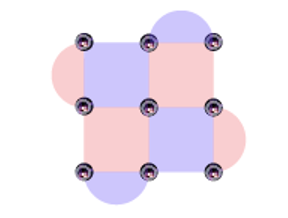
Fig. 1: A schematic logical qubit that resists errors and noise from the environment, built as a cluster of noisy qubits (purple dots) entangled by operations (on extra qubits known as ancillas) represented by the red and purple patches
How do we manipulate information between different logical qubits? The specifics depend on the encoding and decoding processes mentioned earlier, but intuitively, it requires multiple operations among the individual qubits that make up the logical qubits we aim to entangle. During these operations, errors may further appear; they must be detected and corrected accordingly as the calculation proceeds
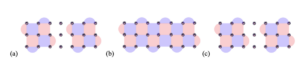
Fig. 2: An example of how logical qubits can be entangled without transversal gates in a surface code. Time flows from (a) to (b) to (c) as the operation happens. Two logical qubit in (a), are assembled and brought to contact via the insertion of extra qubits (in the figure, we explicitly include extra data qubits for clarity). In (b), the logical qubits are entangled via operations between the logical patches, which are subsequently disconnected as in (c). The entangling operations in (b) require measurements, and many rounds of error correction. This process above, called “lattice surgery”, is inefficient and requires stringent hardware performance.
Neutral atoms offer an elegant and efficient solution for entangling logical qubits, known as “transversal gates.” In a transversal gate, by definition, logical qubit operations—whether they are single-qubit or two-qubit operations—are accomplished by applying quantum gates locally to each individual qubit in a single logical cluster.
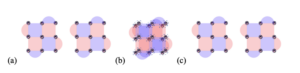
Fig. 3: Via the atom shuttling ability, that allows displacing qubits physically in space while preserving quantum coherence, transversal gates for neutral atoms can be made highly local and parallelized. In the diagram above, time again moves from (a) to (b) to (c). Contrast step (b) with the one in lattice surgery in Fig2. Instead of connecting patches with extra qubits, the two logical qubit patches are physically moved with qubits matching pairwise. Entanglement is generated directly through regular gates between vertices lying close together (blue ellipses). The whole two qubits, at this point, can be entangled with a single laser control beam.
Transversal gates are a potent technique for minimizing errors propagated through the numerous operations required for lattice surgery. In a transversal entangling gate, qubits only interact with their corresponding counterparts, confining errors to specific qubit locations rather than spreading across the system. While this constrained spread of errors is not mandatory for error correction, it strongly saves on rounds of error detection and correction. Consequently, transversal gates can achieve very low error rates, with much more relaxed operation fidelity requirements than alternative approaches, such as lattice surgery (see Fig. 2 above). The convenience and high fidelity of transversal gates could potentially allow the first error-corrected computations to be implemented with much fewer resources than traditional schemes and advance at-scale fault-tolerant quantum computing by years.
The capacity to perform transversal gates is empowered by increased connectivity of operations between qubits, which for neutral atoms can be achieved via developing zoned architectures. These involve moving atoms between three regions: a storage zone where atoms are held, entanglement zone where atoms are reconfigured, and measurement zone where information is extracted from the qubits. Atoms can be transported into and out of different zones to interact with different subsets of qubits. Each zone also requires a very limited number of lasers, roughly independent of how many qubits they operate, so that large-scale systems do not require unreasonable numbers of control channels. The rudimentary features for zoned architectures were demonstrated by researchers from Harvard University, and collaborators, in a seminal paper last year.
Many technical challenges remain. Creating large grid arrays of individual atoms is a complex task, although promising optical trapping techniques are emerging. Precise laser and microwave pulses are essential to achieving high gate fidelities. The progress is ongoing, and as the fidelity and scalability of these systems improves, transversal gates in neutral atoms are likely to play a crucial role in the development of the first quantum computers capable of effectively executing advanced algorithms.
If you found this article to be informative, you can explore more current quantum news here, exclusives, interviews, and podcasts.
















