Insider Brief
- IonQ-led researchers report that simple, symmetry-based cyclic hypergraph product codes outperform machine-optimized and bicycle-type quantum error-correcting codes, suggesting a new route toward more efficient fault-tolerant quantum computing.
- The study finds that cyclic constructions deliver significantly lower logical error rates and cleaner, constant-depth hardware layouts than competing approaches, including codes refined through machine learning and advanced numerical searches.
- Simulations across multiple physical noise levels show that these symmetry-restricted codes maintain strong performance relative to established designs, though questions remain about block-length overhead, decoder behavior, and integration with full logical gate operations.
A team of IonQ-led researchers say they have discovered a surprisingly effective class of quantum error-correcting codes that outperform some of the most optimized designs in use today, suggesting that the path to more efficient fault-tolerant quantum computers could rely on simple mathematical symmetry rather than increasingly complex code engineering.
The findings, presented in a recent IonQ-led study published in the pre-print server arXiv, point to a family of “cyclic hypergraph product” codes that deliver lower error rates and cleaner hardware layouts than competing approaches.
The study indicates that these codes, which are constructed by combining classical cyclic codes in a structured way, rival or surpass more elaborate low-density parity-check codes that have been refined through machine learning and advanced numerical searches. The researchers attribute the improvement not to new algorithmic tricks but to the power of imposing global symmetry across the code structure, which makes the codes easier to search, easier to implement and unexpectedly more resilient to noise.

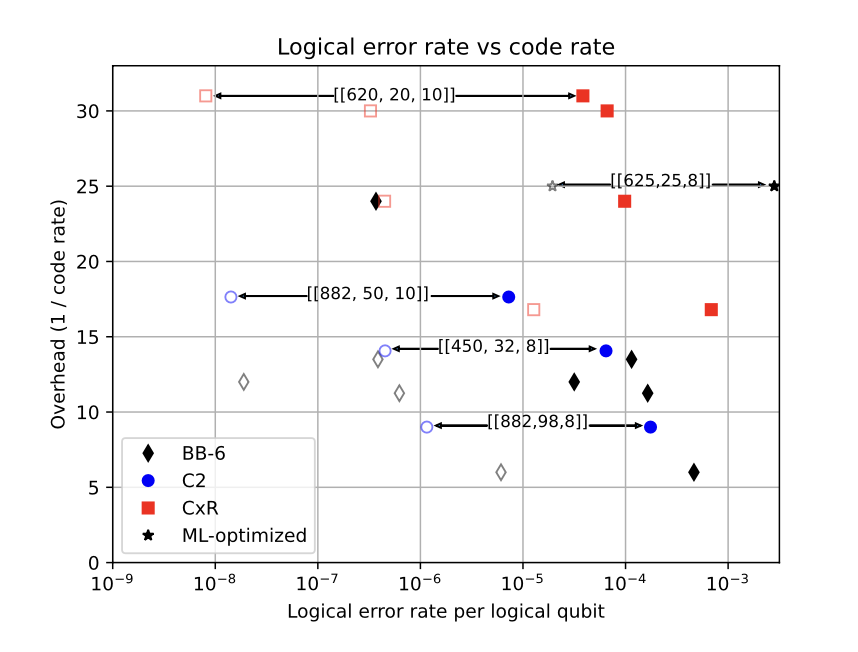
To illustrate the difference, the researchers compare several specific code constructions.
“Our circuit level simulations with physical error rate equal to 10⁻³ show that cyclic HGP codes perform far better than the ML-optimized HGP codes,” the team writes. “We found a [[882, 50, 10]] C2 code that achieves a logical error rate per logical qubit below 2×10⁻⁸ where the ML-optimized [[625, 25, 8]] code of [18] only achieves ≈2×10⁻⁵. Another example is a [[450, 32, 8]] C2 HGP code which reaches the same minimum distance as the previous ML-optimized HGP codes with shorter block length and more logical qubits. Moreover, it achieves a logical error rate per logical qubit of 4.5×10⁻⁷. Surprisingly, despite their very simple structure, even the CxR codes achieve a significantly better logical error rate per logical qubit than the ML-optimized HGP codes.”
The researchers report the results add weight to the view that quantum error correction — which is a highly sought, critical ingredient in any large-scale quantum machine — may still have untapped opportunities for performance gains through structural insights rather than brute-force optimization.
The study also highlights advantages for practical hardware layouts, which could matter as quantum systems scale beyond experimental prototypes.
How Cyclic Codes Work
Quantum computers are notoriously sensitive to small disturbances. Error-correcting codes protect the underlying data by spreading information across many physical qubits in a way that allows errors to be detected and reversed. Hypergraph product codes, introduced more than a decade ago, are one family of codes known for offering strong theoretical guarantees. But in practice, they require careful layout and decoding strategies to compete with the more widely known surface codes used today.
Most recent improvements have come from tuning these codes through randomized searches or machine-learning techniques that modify the structure of the underlying classical codes.
The IonQ team took a different approach. Instead of letting algorithms wander through a huge search space of possibilities, they restricted the construction to codes built from cyclic patterns — or, mathematical structures that repeat with a fixed rhythm. That symmetry drastically reduces the number of options the search has to consider, allowing the team to perform a complete enumeration of all cyclic codes of small size and select the best combinations.
According to the study, the resulting “C2” and “CxR” families of codes — both built using cyclic ingredients — achieved logical error rates far lower than previous hypergraph product codes optimized by random walks, simulated annealing or reinforcement learning. In some cases, the cyclic codes delivered error rates several orders of magnitude lower than machine-optimized examples with comparable resources.
The researchers also found that some cyclic constructions matched or outperformed bivariate bicycle codes, a newer class of quantum codes that are known for their strong performance and compact layouts. Although the cyclic codes sometimes require larger block lengths, they offered combinations of lower error rates and smaller overhead in several regimes tested in the study.
Why This Matters for Scalable Quantum Machines
For quantum computers to become practical, they must run error-correcting cycles many times per second, often with limited time to perform gates. Code constructions that lead to simple, regular layouts can reduce hardware demands and simplify the control system.
The study shows that the cyclic structure produces a clean, two-line layout of qubits and their measurement partners, known as ancilla qubits, arranged in a repeating pattern that is easier for hardware to execute. That pattern allows all stabilizer checks — the measurements that detect errors — to run in constant depth, meaning the time required for one round of error detection does not grow as the code scales. The researchers state that this is especially compatible with architectures that move qubits, such as trapped ions, photonic qubits or neutral atoms.
This constant-depth property matters because longer circuits introduce more opportunities for noise. Codes that maintain short, regular circuits tend to perform better on real hardware, even if their abstract mathematical parameters are similar to competing designs. The study points in the direction that the combination of symmetry and structure in cyclic codes leads to circuits with balanced weight, efficient packing and no idle qubits between layers. All of this could help reduce accumulated noise during error detection.
What the Researchers Did
To conduct the study, the team exhaustively catalogued all classical cyclic codes with small check weights and short lengths, filtering out those with poor performance.
They then constructed hypergraph product codes from these classical components and simulated their performance at the circuit level, using a standard noise model and a widely used stabilizer-circuit simulator. The study reports results across a range of physical error rates, showing how the logical error rate — the probability that the encoded data is corrupted — changes as noise increases.
The simulations compared the new codes to machine-optimized hypergraph product codes and to recent bicycle-type codes. In many cases, the cyclic constructions maintained lower logical error rates for similar overhead, defined as the number of physical qubits per logical qubit. The researchers emphasize that these results hold for circuit-level simulations, which more closely represent real hardware than simplified code-capacity models.
The study also demonstrates a layout procedure for constructing the required circuit using only cyclic shifts and local interactions. This is intended to show that the codes are not only good on paper but also suitable for physical implementation.
Limitations and Open Questions
As with any coding scheme, tradeoffs remain between code size, resource overhead and implementation complexity. The study suggests that many of the best-performing cyclic constructions require larger block lengths than competing bicycle codes, which could increase hardware demands in early machines. Cyclic symmetry improves performance and layout simplicity, but it also constrains possible code shapes, meaning that some potentially strong designs may not be captured in the restricted search space.
Another limitation is that the study focuses on memory performance — how well the codes hold a quantum state — rather than full logical computation. Implementing logical gates fault-tolerantly is a separate challenge, and the researchers acknowledge that future work must extend these constructions to include gate operations. Previous research on hypergraph product codes provides some starting points, but additional engineering will be required to integrate the new cyclic family into a full fault-tolerant stack.
The simulations also rely on a particular noise model and decoding strategy. Real hardware may exhibit different error behaviors, and decoders tuned to cyclic symmetry may offer further gains or reveal new constraints. The study does not claim to have proven optimality; it instead shows that symmetry-restricted searches can uncover high-performing codes that previous approaches overlooked.
Next Steps And Future Work
The researchers say the results broaden the design space for quantum error correction by showing that global structure can matter as much as local optimization.
The next steps include exploring logical gate implementations, integrating the codes with hardware-specific control systems and testing their performance on emerging trapped-ion and photonic architectures that can naturally implement the required cyclic shifts.
If the performance advantages hold on physical systems, the cyclic hypergraph product family could become a contender for future large-scale quantum computers. The study concludes that the combination of simplicity, symmetry and implementation efficiency makes these codes a promising direction for long-term quantum memory designs and potentially for full fault-tolerant computation.
The research team included Arda Aydin, Nicolas Delfosse and Edwin Tham.
For a deeper, more technical dive, please review the paper on arXiv. It’s important to note that arXiv is a pre-print server, which allows researchers to receive quick feedback on their work. However, it is not — nor is this article, itself — official peer-review publications. Peer-review is an important step in the scientific process to verify results.