Insider Brief
- A research team in China has developed a quantum search algorithm that extends Grover’s quadratic speedup to continuous optimization and spectral problems.
- The algorithm rigorously proves quantum speedup for searches over uncountably infinite solution spaces and establishes a lower bound confirming its optimality.
- The team also designed a general framework for building quantum oracles, enabling broad application in high-dimensional optimization and infinite-dimensional spectral analysis.
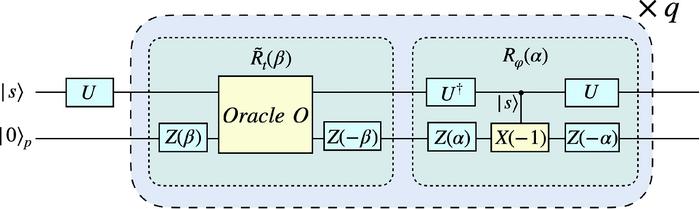
- Image: The quantum circuit of the proposed quantum search algorithm for continuous search problem. (Science China Press)
PRESS RELEASE — A search problem refers to the task of finding a solution within some space of possible options, and that space could be made up of discrete steps or continuously varying values. For example, solving a maze is a typical discrete search problem, while robot path planning (where the robot can move in any direction and at any speed) is a continuous search problem.
In real world, many problems—ranging from high-dimensional optimization to spectral analysis of infinite dimensional operators—require searching over continuous, uncountably infinite solution spaces, which introduces huge computational complexities not present in discrete problems. With the advent of quantum computing, such continuous search problems have gained new momentum due to the potential for quantum speedup. For example, Grover’s quantum search algorithm offers a quadratic speedup compared to classical algorithms. However, most established quantum search algorithms primarily focus on discrete search problems, and extending these algorithms to continuous search problems remains an active area of research.
Recently, a research group from the University of Electronic Science and Technology of China has proposed a novel quantum search algorithm tailored for continuous optimization and spectral problems. In this algorithm, the researchers successfully extended Grover’s quadratic query speedup to the continuous domain, rigorously proving that their method achieves the quadratic speedup. Moreover, they established a lower bound on the query complexity for quantum search in continuous settings, confirming the theoretical optimality of their algorithm.

Beyond the theoretical foundations, the researchers provided a detailed framework for constructing and implementing the quantum oracle required for the search algorithm, demonstrating its adaptability across a wide range of applications, including continuous optimization and spectrum calculation for complicated operators over infinite Hilbert space. As experimental advances in continuous-variable platforms continue, this work is poised to become foundational for quantum algorithms tackling continuous search problems at scale.
See the article: Fixed-point quantum continuous search algorithm with optimal query complexity.