Insider Brief
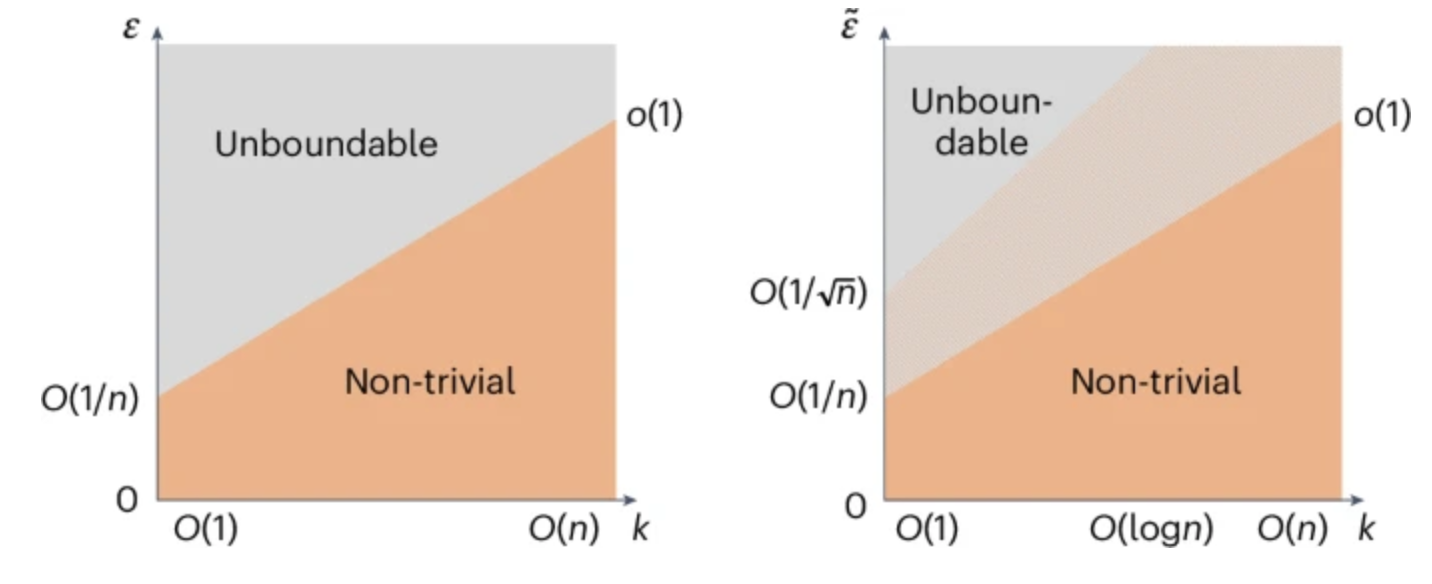
- Researchers at the Perimeter Institute have developed a mathematically rigorous method to distinguish nontrivial quantum error correction (QEC) codes from trivial ones, offering a new way to assess quantum systems’ behavior and improve error correction techniques for reliable quantum computing.
- The new framework has potential applications in condensed matter physics, particularly in the study of topological order in quantum materials, and provides insights into the relationship between entanglement conditions and code properties.
- The study also extends to the integration of quantum mechanics with Einstein’s theory of general relativity, using AQEC codes and Conformal Field Theory systems to explore new pathways for understanding quantum gravity.
Researchers at the Perimeter Institute for Theoretical Physics report they have identified a new method to distinguish nontrivial quantum error correction (QEC) codes from trivial ones, which may not only be a significant advance in the quest for reliable quantum computing, but a new way to probe some of physics’ biggest challenges.
The team, published their findings in Nature Physics, revealed a mathematically rigorous boundary that clarifies how quantum systems behave in real-world conditions. This new method will aid in improving the accuracy and reliability of quantum systems, which are central to solving complex scientific and technological problems.
Quantum error correction (QEC) is essential for protecting quantum information from noise and errors, which is considered a hurdle in making quantum computers practical. The new research connects the properties of Approximate Quantum Error Correction (AQEC) codes to the complexity of quantum circuits, showing that this relationship is not arbitrary but rooted in the physical behavior of quantum systems. The discovery promises to impact not only quantum computing but also fields like condensed matter physics and quantum gravity.

“This new dividing line that we’re proposing between acceptable and unacceptable codes corresponds to something physically meaningful,” said Dr. Daniel Gottesman, one of the researchers involved in the study and a long-time faculty member at Perimeter Institute, in a statement. “It shows that this was not just some random thing that we came up with, but that it’s connected to something fundamental.”
The paper, written by Gottesman, Jinmin Yi, Weicheng Ye and Zi-Wen Liu, provides a rigorous mathematical framework for evaluating AQEC codes. These codes, which allow for a certain margin of error, are increasingly being recognized as critical for quantum computing’s future applications. The researchers introduced a concept called “subsystem variance,” a parameter that can be used to evaluate the precision of AQEC codes. The findings suggest that AQEC codes emerge naturally in a variety of quantum systems, opening up possibilities for improving both theoretical understanding and practical applications of quantum error correction.
You could think of this emergence as noise-canceling headphones. Just as the headphones don’t completely eliminate all background sound but reduce it to a tolerable level, these AQEC codes function don’t completely correct all quantum errors, but they can reduce the effects of noise or disturbances in the quantum system to an acceptable level. So, in both cases, the system — whether the noise-canceling technology or the quantum error correction code — can handle a certain amount of noise while still functioning effectively. In AQEC codes, the “noise” is quantum errors, and the system is designed to tolerate small errors, allowing quantum information to be processed with sufficient reliability without requiring exact correction.
Beyond Quantum Computing
In addition to quantum computing, the research has implications for condensed matter physics, particularly in the study of topological order, according to the Perimeter Institute article about the team’s work. Topological order involves the intricate properties of quantum materials like fractional quantum Hall states and certain types of superconductors. The new framework allows researchers to better understand the relationship between entanglement conditions and quantum code properties, potentially offering insights into the behavior of these exotic materials.
Jinmin Yi, a doctoral student at Perimeter and co-author of the paper said in the statement that their research has provided “a quantitative understanding of why these two notions are actually different.”
This could build the foundation that will unlock new directions for future research.
“The entanglement conditions and the code property conditions are often lumped together in the community, and there has been little understanding about their relationship,” said Yi. “So our work provides a quantitative understanding of why these two notions are actually different – we gave a mathematically rigorous way of defining it.”
Einstein’s Unfinished Business
The implications extend beyond condensed matter to one of the most challenging problems in physics: the integration of quantum mechanics with Einstein’s theory of general relativity. While quantum mechanics governs the behavior of the smallest particles, general relativity explains the force of gravity and spacetime on a cosmic scale. These two frameworks operate on fundamentally different principles, and merging them into a unified theory has proven difficult due to contradictions in how they describe space, time and matter.
The researchers’ analysis of AQEC codes using subsystem variance could provide new insights into Conformal Field Theory (CFT) systems, which describe quantum fields that behave consistently across different scales and are thought to be related to gravitational descriptions in certain theoretical frameworks.
“There has been extensive research into how to use quantum error-correcting code to study holographic systems, but mostly people are just playing with toy models based on exact codes that fail to capture key CFT properties,” said Yi. “Our work first studies the code properties of CFT systems, and we give a rigorous description of such CFT codes in relation to intrinsic features of CFT, revealing their approximate nature. The analysis potentially gives new insights about what kind of CFT systems are accompanied by a gravity dual.”
While these results are encouraging, they represent only an initial step in understanding the full scope of AQEC codes and their applications, according to the team. Future research is expected to focus on refining these findings and exploring their utility in more complex quantum systems.
In one path, specifically for the quantum computing community that is guiding the evolution of quantum devices, improving error correction will be needed to achieve practical and reliable quantum systems. This new boundary for AQEC codes offers a promising path forward, helping these researchers and engineers develop systems that can handle the inherent noise in quantum computing processes.
The research also opens up several avenues of exploration, from better understanding the physics of topological order to improving the accuracy of quantum gravity models.
“Physicists have been applying ideas from the field of quantum information to study physical scenarios for a long time,” said Liu. “They have been thinking about topological order as fundamentally a quantum error-correcting code, or in the field of holography, people talk about ‘holography code’. In most of the cases, the model that they are studying is intrinsically an exact code. But in real life, there are all kinds of imperfections, deviations, and more fundamental reasons such as symmetries or physical nature that render AQEC codes.”