Microsoft researchers reported earlier this year that they took a scientific leap in demonstrating the underlying physics of creating a topological qubit. But, they realize that leap is really just a step toward scalable quantum computers using that modality.
Now, the team said they’re ready to address improvements across the stack, according to a research blog post.

They write: “… our quest to deliver a general-purpose quantum computer capable of addressing industrial-scale problems will require innovation across every layer of the quantum stack, from materials at the nanoscale to algorithms and applications. At Azure Quantum, our full-stack approach and broad expertise across all areas of quantum computation allows us to drive innovation in this space through tight collaboration across theory, hardware, software and systems teams.”
According to the post, the researchers focused on creating an error correction code for topological qubits, which is a focus of much of Microsoft’s quantum efforts. The qubits in quantum computers — and topological quantum computers are no exception — are so sensitive that any number of environmental interferences, or noise, can throw off their calculations. For the Microsoft team, the key may be in having code that “flows” over time rather than statically “floats” in place, so to speak.

“At Azure Quantum, our full-stack approach and broad expertise across all areas of quantum computation allows us to drive innovation in this space through tight collaboration across theory, hardware, software and systems teams.”
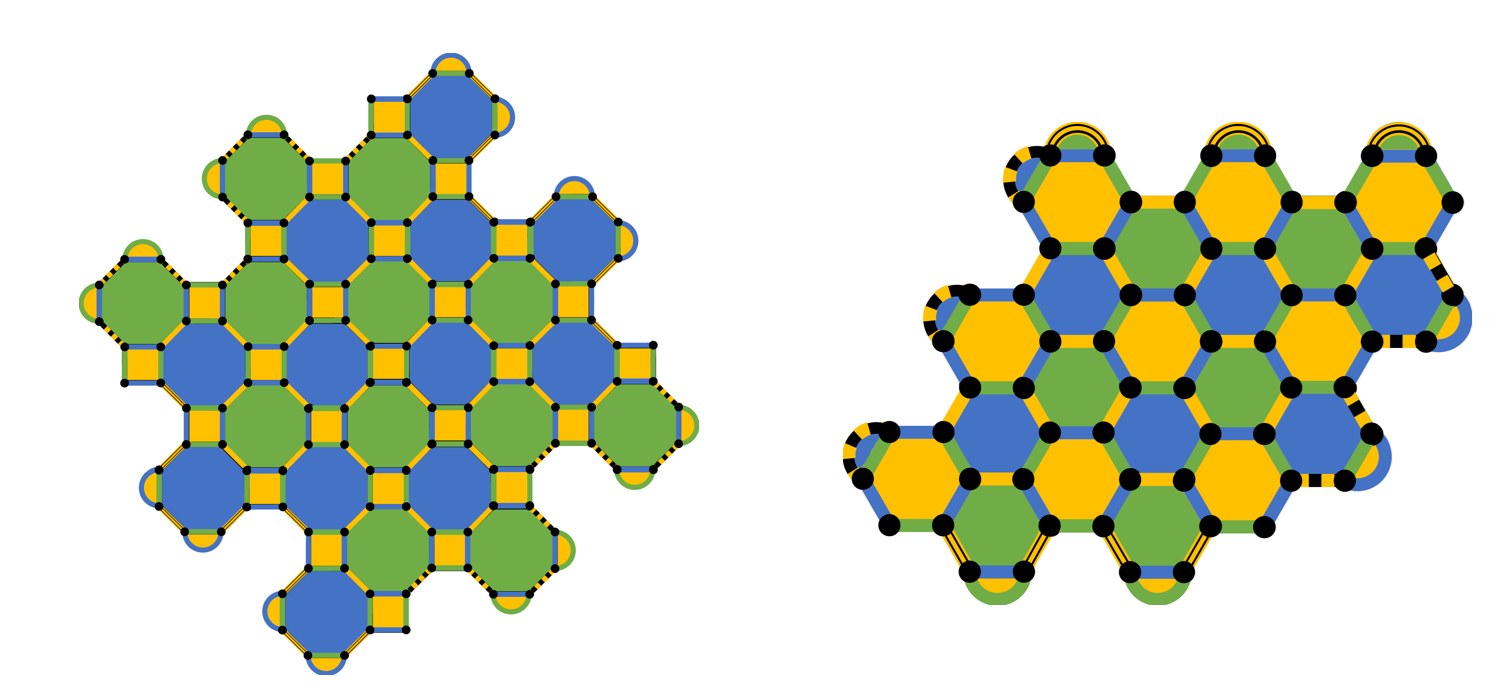
“Our recent breakthroughs overcome this issue through a conceptually new perspective on quantum codes (put forward in “Dynamically Generated Logical Qubits” and “Boundaries for the Honeycomb code”), where the encoding of the quantum information is not static but rather allowed to periodically evolve in time,” the researchers write. “Many examples of physical systems are known where such periodic evolution allows new phenomena to occur (see, for example, the well-known Kapitza pendulum). The study of such systems falls under the term Floquet systems, which gives this new class of codes its name.”
The codes are built entirely from two-qubit measurements referred to as “check measurements,” which are used to, as you might guess, check for errors. However, in this scheme, after a check is measured, the encoding of the quantum information is changed. The measurement outcomes, then, cannot be used directly to infer which errors have occurred, but take into account the full history of measurement outcomes over time.

The researchers believe that Floquet codes leads to better, more efficient error correction and the need for fewer physical qubits to build a logical qubit. Ultimately, that represents a step toward quantum advantage.
According to the researchers: “Along with our recent demonstration of the building blocks for topological qubits, optimizing quantum error correction using Floquet codes represents a critical piece of the scientific foundation needed to achieve scaled quantum computation. These breakthroughs help establish a path and architecture for the industrial quantum machine.”
The Microsoft research team includes Bela Bauer, Matthew Hastings and Jeongwan Haah.
For a deeper technical dive, please see the Microsoft Research Blog.
For more market insights, check out our latest quantum computing news here.