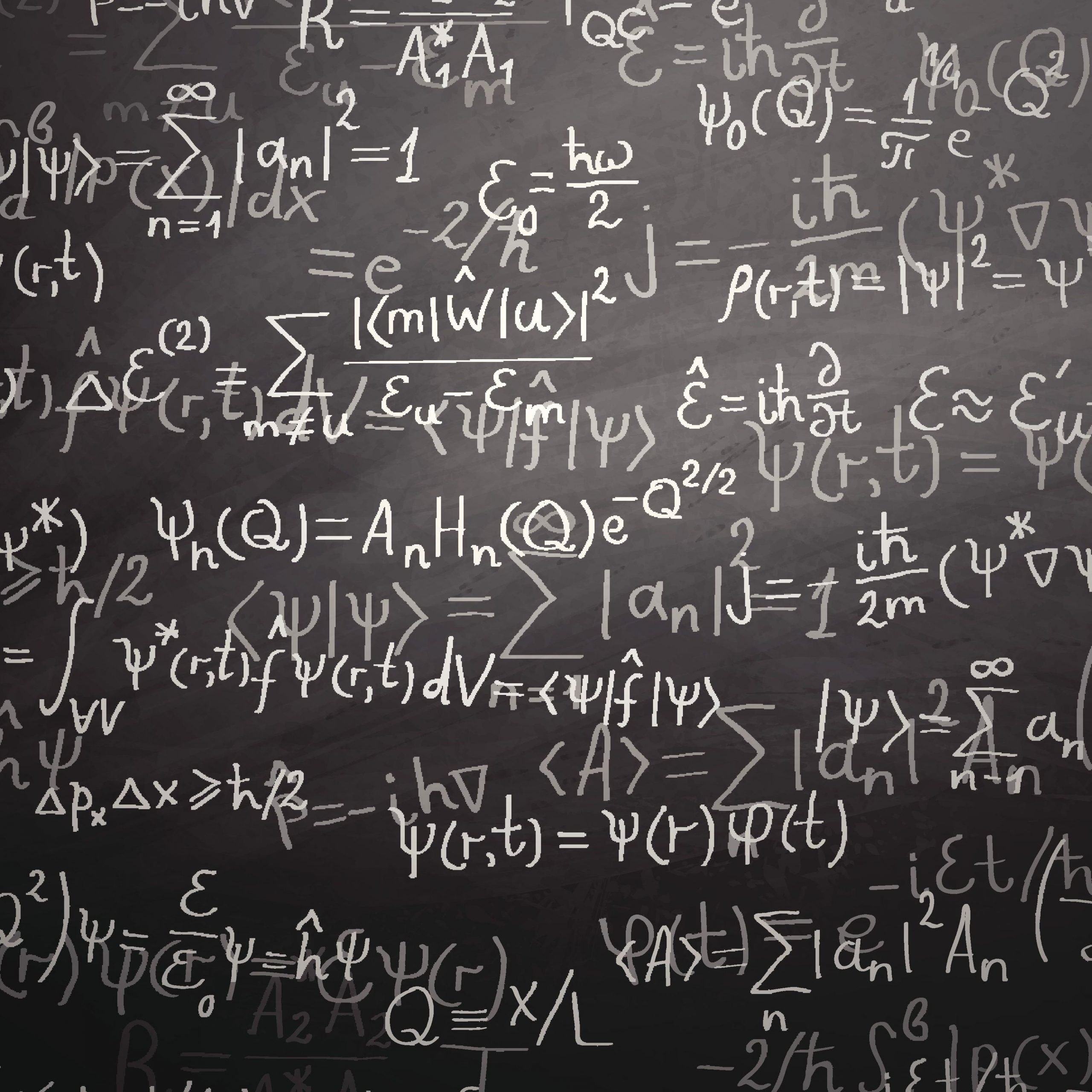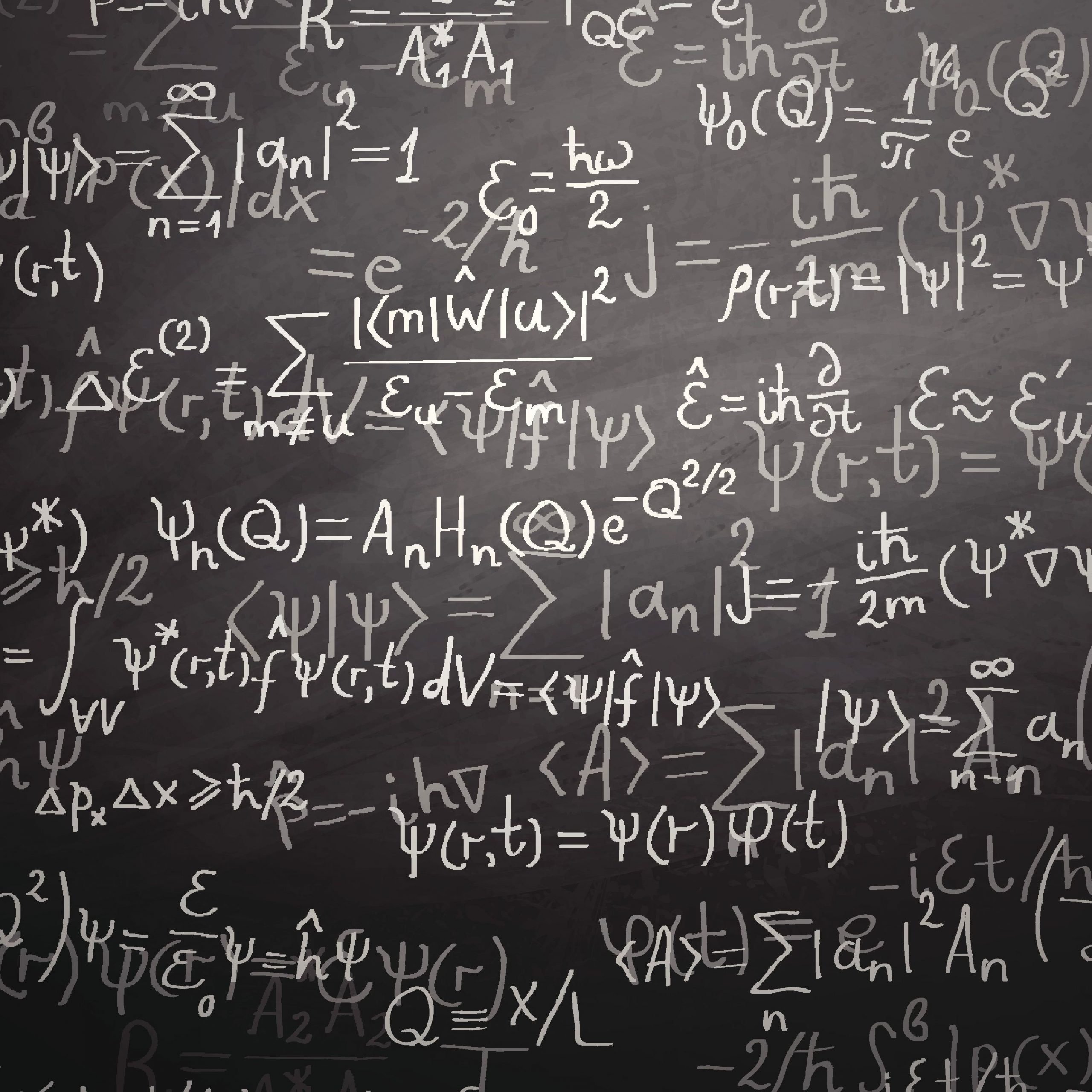
Research from Yale University, newly published in Annals of Physics, has established that we can unify the ways in which we describe measurements in classical physics and quantum physics.
When Feynman was not saying that “nobody really understands quantum mechanics,” he was, in contrast, saying, “The physicist needs a facility in looking at problems from several points of view.” When considering different points of view, it is much better to understand in as much detail as possible how they relate to each other, so that we can build a way in which they can be unified.
Hidden Measurements

Remarkably after almost a century, it is only recently that we can recognize that classical physics can be extended by the introduction of what we might call “hidden measurements” so that an extended form of classical physics can be unified with quantum physics. These “hidden measurements”, which describe how to transform between different classical points of view, have always been present in classical physics. For decades they have been used routinely in classical signal analysis, but they may not be used in classical physics.
What is a “measurement?” In a signal analysis picture, a modern experiment has many wires in and out of it, which we can call “signal lines” because each of them carries a “signal”. We would see a “signal” as a bright line if we connected the wire to an oscilloscope. At every moment, the height of that bright line is the measurement result for that wire at that moment. In modern experiments, that height is examined by hardware many billions of times per second.
There is always a lot of noise, which would need us to record Terabytes of data per second. Instead, hardware makes an elaborate decision whether the signal satisfies a “trigger”, and records only the times of those events, which is a very lossy compression indeed. At the level of the signal, there is no “collapse of the wave function”, there is just a signal on a signal line, but at the level of the hardware compression much information is lost.
Transformations
We can transform measurements in nontrivial ways using either hardware or software, for example using a diffraction grating or Fourier analysis to discover which frequencies are prominent in a signal. Such transformations are a commonplace in signal analysis, which introduces the mathematics of Hilbert space, which pulls together both the extended form of classical physics and quantum physics into a single picture. In the simplified context where there is no noise, four videos capture why classical physics becomes more complicated if we allow all the tools of signal analysis, from the well-known YouTube channels 3Blue1Brown, Minute Physics, Sixty Symbols, and The Science Asylum.
If we use the “hidden measurements” of classical physics, which as transformations are unlike the usual classical measurements but are much like the quantum measurements we use routinely, then we don’t need quantum physics. It’s better, however, to follow Feynman’s advice and know how to discuss experiments in both ways and how to translate between them, because they are different.
With the extended form of classical physics, using all the transformation tools of modern signal analysis, we can follow to the letter Niels Bohr’s insistence that we must classically describe an experiment, its results, and all the signal analysis that must be done to make sense of the results.
What is missing?
In the first instance, there are no particles or waves, there are only many measurement results, very few of which are ever seen by a person. Only when measurement results are completely compatible with supposing that a particle passed by should we think that perhaps a small part of the signal, the almost negligible part that was recorded, was caused by a particle. The discarded part of the signal is something else. We’ve known for most of the last century that thinking about particle properties of position and momentum leads to extreme problems, so it’s time to put them aside.
There is a tide of attempts to make sense of quantum physics in the physics literature, only very few of which make it into popular science articles and books. I have a friend who is quite sure that “quantum logic” solved all these problems in the 1980s, and he’s very nearly right; there is an interpretation called “consistent histories” that almost tells the same story as here; the quantum computing idea of non-demolition measurement gives a hint of a classical way to approach quantum computing; and Gerard ‘t Hooft and Stephen Wolfram are only two of the physicists who have been arguing for decades that classical physics is as good as quantum physics for describing experiments, and that chaos theory holds the key to understanding how classical physics and quantum physics are related.
There are many reasons, however, why none of these approaches have taken hold. It is therefore only right to be cautious of the above: despite its new approach, focused on signal analysis and an extended classical physics, this is just one more attempt to make physics make sense. But remember Feynman: you now have the beginning of a new way of thinking and how to translate it into others. If your head doesn’t overload, that gives you an advantage.
In a second post, quite independently, we’ll see how to unify “Collapse” and “No-Collapse” interpretations of approaching quantum physics. That is in some ways a bigger deal.
The published version of the article in Annals of Physics that underlies the above, “An algebraic approach to Koopman classical mechanics”, may be found here [which may be downloaded free until April 2nd, 2020, using this link.] A preprint that is fairly close to the published version may be found here.