By Pedro Lopes, Alexei Bylinskii
QuEra Computing
Beyond increasing the number of qubits or achieving longer quantum coherence times, mid-circuit readout is a critical factor in enhancing the capabilities of quantum computers.
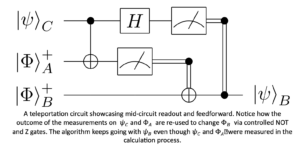
Mid-circuit readout (MCR) refers to the ability to selectively measure the quantum state of a specific qubit or a group of qubits within a quantum computer without disrupting the ongoing computation. In some algorithms, these measurement results can also be reincorporated into the ongoing calculation, affecting it in a process known as “feed forward.” One of the most prominent applications of MCR is in quantum error correction for fault-tolerant quantum computers.
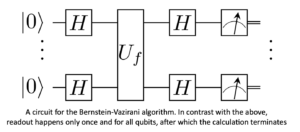

A circuit for the Bernstein-Vazirani algorithm. In contrast with the above, readout happens only once and for all qubits, after which the calculation terminates
The ease or difficulty of implementing MCR capabilities in a quantum computer depends on the chosen physical platform and architecture. At the time of this article, architectures based on superconducting qubits, trapped ions, and neutral atoms have all demonstrated MCR in a limited context. The neutral-atom platforms, in particular, are poised to apply MCR for error correction at scale, and in the following discussion, we will explore the strengths and challenges of MCR for neutral atoms.
Presently, neutral-atom quantum computers determine calculation results through a destructive qubit readout process: atoms are illuminated with laser light. Those in state 1 are ejected, and those in state 0 emit fluorescence which is detected on a camera. The camera image is processed to determine a given qubit state based on the brightness of pixels corresponding to it. In an optimized system, this process detects the correct qubit state with 99.9% probability. If one wants to use this process for MCR as is, all that is necessary is to target individual atoms with the laser light that generates fluorescence.
There are two difficulties this setup introduces. The first is the loss of qubits in state 1. This does not scale well for applications where many rounds of MCR are required, such as in most error-correction protocols. The second problem is that the light scattered in the imaging process can impinge on the atoms that were not targeted by the imaging laser beams for readout, introducing decoherence and preventing the quantum computation from continuing. For error-correction applications, in particular, this kind of readout destroys the ‘ancilla’ qubits (meant to be detected) and destroys the superposition of ‘data’ qubits (meant to continue the quantum computation forwards after the MCR).
Both problems can be solved by leveraging the capacity of shuttling atoms around with the same type of lasers (“optical tweezers”) that hold them in the first place. That way, qubits to be measured can be shuttled to a dedicated readout zone, well-separated from the remainder qubits, where they can safely scatter the imaging light without perturbing the computation. To complete the solution after the MCR, one can again move pre-loaded and pre-initialized atoms from a separate reservoir to replace the ejected measured atoms. Particularly at scale, when many atoms are tightly packed, there is arguably no solution more elegant than this.
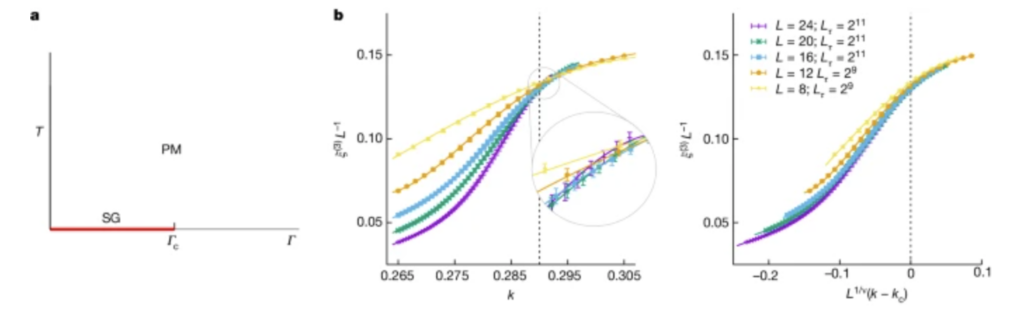
Atom transport of this kind has recently been shown to preserve qubit coherence and to be highly parallelizable in 2D. In a seminal work by Dolev Bluvstein, from Harvard University, and collaborators, atom transport of this kind has recently been shown to preserve qubit coherence and to be highly parallelizable in 2D. It is fast enough to allow more than 10,000 shuttling operations within the coherence time of a neutral atom qubit, and it has enough range to span more than 10,000 qubits packed in 2D. Together with the zoned layout, this enables a QPU architecture with vastly simplified control requirements, optimized performance for each computational primitive, and starts to resemble classical CPUs. Drawing inspiration from classical computer architecture, which has separate memory and computation units, such a quantum architecture can consist of three different functional zones: storage, entangling, and readout. The storage zone is used for qubit storage, featuring long coherence times; the entangling zone is used for high-fidelity parallel entangling gates, operating on the qubits; and the readout zone gives us the capability to measure the quantum state of a subset of qubits without affecting the quantum state of other qubits, which is critical for error correction.
In the context of MCR, the number of ancilla that can be moved into the readout zone and detected simultaneously can be optimized for the algorithm at hand, and the isolation of the readout zone from the processing zone can be optimized for the desired performance on ancilla detection fidelity and on data qubit coherence.
The real power of MCR comes with the alluded feed-forward processes. These come with challenging requirements on the part of classical data processing. Raw data needs to be read in, processed in the context of the algorithm or error correcting code at hand (also known as ‘decoding’), then control signals destined for the data qubits need to be updated, and the whole loop must be executed fast and many times over. For fault tolerance, the correction of errors implemented by this process must win the race against decoherence, putting stringent requirements on the latency of this pipeline, which can be addressed with classical firmware that is tightly coupled to the data acquisition and control signal generation devices.
While many of these aspects still need to be engineered into a cohesive system and useable platform to be made available to developers and users, they are relatively close for neutral atom architectures. With the right approach, neutral atom quantum computers can become truly scalable quantum machines, enabling a wide range of new algorithms and applications.
If you found this article to be informative, you can explore more current quantum news here, exclusives, interviews, and podcasts.