Guest post by Alex Lukin, Tommaso Macri, QuEra Computing Inc.
Quantum computing holds the promise of revolutionizing information processing. At its core are qubits, the fundamental units of quantum information. However, there’s a catch: qubits are astonishingly delicate and require careful shielding from their surroundings. Understanding and extending their coherence time—the duration they maintain their quantum state—is paramount.
The Quantum Lifespan
Coherence time is a fundamental metric in the world of quantum computing. It’s akin to the lifespan of a qubit, measuring how long, on average, this object can preserve its intricate quantum state.
The main difference between qubits and classical bits lies in their ability to exist in a superposition of cardinal states and, more importantly, the presence of phase between those states. This phase is what grants qubits their superior computing power over classical bits. However, it also renders qubits fragile compared to classical bits, as any disturbance from the environment can lead to the collapse of superpositions and scrambling of phase over time. Coherence time quantifies how long a qubit can maintain its superposition and phase coherence properties.

Since we’re tracking two distinct components (superposition and phase coherence), there are two separate values describing the qubits: T1 and T2. T1 indicates how long it takes for the amplitude of the superposition to decay, or in other words, how long it would take for a qubit initially in state 1 to decay to 0. On the other hand, T2 reveals how long it takes for a phase between states in superposition to shift. It turns out to be an extremely sensitive quantity as even minuscule disturbances in the qubit’s environment result in these phase shifts, causing the qubit to lose its quantum information over time. Consequently, it’s often referred to as “qubit coherence” without additional qualifiers. T2 is always limited by T1, in some platforms, such as superconducting qubits, this limit has been reached, whereas in others (neutral atoms and ions) T1 is much greater than T2 which give a much easier path for improvement by addressing the sources of technical noise in the system. Some emerging quantum platforms, such as topological qubits, aim to shift the paradigm by encoding phase information into distributed degrees of freedom of the system, requiring correlated noise throughout the system to cause unlikely errors. Unfortunately, a robust demonstration of such a qubit remains elusive to date.
It’s important to note that coherence time in absolute physical units (e.g., seconds or microseconds) is less relevant as a metric for comparing platforms. The reason is that we want to perform operations on the qubits, specifically two-qubit entangling operations, which vary drastically in duration across different platforms. Therefore, the relevant metric is the number of two-qubit operations achievable within the coherence time, which can be determined by the ratio of T2 to the gate operation duration. For instance, while superconducting qubits might have only 30µs of coherence time compared to 1000µs for trapped ion systems, once we consider the duration of the gate, superconductors can perform nearly twice as many operations within the coherence time compared to ions.
The number of gate operations is one area where neutral-atoms computers might have a distinct advantage.
Coherence times in neutral atoms
Let us delve deeper into the realm of neutral atom systems. The most common method of encoding of qubit states in these systems employ hyperfine states. Hyperfine states are discrete energy levels within an atom’s electronic structure. They exhibit remarkable stability and resilience against environmental perturbations, making them prime candidates for qubit encoding. For neutral rubidium atoms, qubit states encoded in the ground state correspond to electronic states with a principal quantum number of n=5, with no net orbital angular momentum and two different hyperfine states (labeled with the quantum number F, for example, F=1 and F=2). Two-qubit gates are achieved by coupling one hyperfine state to a highly-excited electronic state (n>>10) called the Rydberg state. Large principal quantum numbers ensure strong interactions between the atoms and, consequently, fast entangling gates.
In neutral rubidium atoms, qubit states are encoded in the ground electronic state, which is characterized by a principal quantum number of n=5. The principal quantum number is a crucial quantum mechanical attribute that specifies the energy level of an electron in an atom. It essentially defines the “shell” in which an electron resides, and higher values of n correspond to higher energy levels and greater distances from the nucleus. In the case of rubidium, the ground state has a principal quantum number of n=5, indicating that the electrons in this state are in the fifth energy shell.
Comparing various modalities
In the table below, we compare the absolute coherence times, two-qubit gate durations, and the number of operations for the major quantum computing platforms: Ions, superconducting systems, and neutral atoms. Superconductors facilitate swift operations, albeit with a much smaller T2 coherence time. Neutral atoms operate at a lower rate but surpass other platforms in total operations.
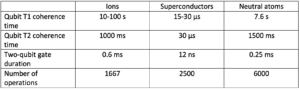
In fairness, it is important to note that while neutral atom platforms offer unique advantages such as high qubit connectivity and long coherence times, they also come with some inherent challenges, particularly concerning cycle times. One significant drawback is the time required to arrange individual atoms into a specific geometric configuration using optical tweezers or magnetic traps. This process can be time-consuming and may limit the overall speed of quantum operations. Also, using camera-based detection systems to analyze each atom’s state introduces another layer of latency. The camera needs to capture and process images to read out the quantum states, and this image analysis can be both computationally intensive and time-consuming. As a result, the overall cycle time—the time it takes to prepare, execute, and read out a quantum operation—can be considerably longer compared to other quantum computing platforms like superconducting qubits or trapped ions.
Conclusion
In conclusion, the pursuit of quantum computing hinges on the delicate balance between qubit coherence and operational speed. Coherence times stand as critical parameters, reflecting a qubit’s ability to maintain superposition and phase coherence. While superconductors offer rapid operations, their limited T2 coherence time poses a challenge. In contrast, neutral atom systems, leveraging stable hyperfine states, demonstrate impressive T2 coherence times and excel in the total number of operations performed within this window. This distinction, among other relevant features, positions neutral atoms as a promising frontier in quantum computing, offering a compelling avenue for future advancements in this transformative field
For more market insights, check out our latest quantum computing news here.
Resources/References
Ions: https://ionq.com/resources/ionq-aria-practical-performance
Superconducting qubits: https://www.nature.com/articles/s41586-022-05434-1
Neutral atoms: https://arxiv.org/abs/2304.05420