The era of quantum computers — and their ability to cultivate both constructive and destructive applications — may be upon us.
In a study, a team of Chinese scientists report they were able to create an algorithm to factor factor integers up to 48 bits with just 10 superconducting qubits. Most experts believed the task would take millions of qubits.
The team suggests that the experiment shows that public key cryptographic techniques that rely on integer factorization may soon be vulnerable to even the primitive NISQ — noisy intermediate scale quantum — computers of today.
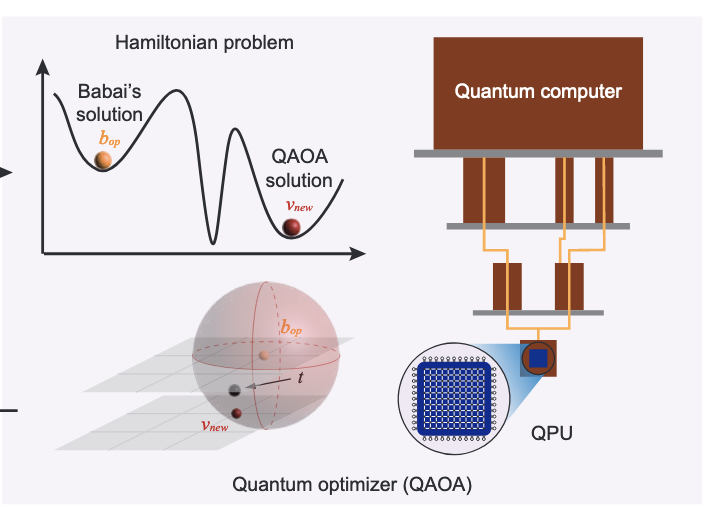
According to the researchers, The algorithm is based on the classical Schnorr’s algorithm, which uses lattice reduction to factor integers while relying on quantum approximate optimization algorithm — or QAOA — to optimize the most
time-consuming part of Schnorr’s algorithm to increase the speed of the factorization progress.
“Using this algorithm, we have successfully factorized the integers 1961 (11-bit), 48567227 (26-bit) and 261980999226229 (48-bit), with 3, 5 and 10 qubits in a superconducting quantum processor, respectively. The 48-bit integer, 261980999226229, also refreshes the largest integer factored by a general method in a real quantum device,” the researchers write.

They add that near-term quantum computers that use this algorithm may be able to handle much larger integer factorization problems — and break the widely used RSA-2048 cryptographic scheme used to protect computer data and systems.
The researchers write: “We proceed by estimating the quantum resources required to factor RSA-2048. We find that a quantum circuit with 372 physical qubits and a depth of thousands is necessary to challenge RSA-2048 even in the simplest 1D-chain system. Such a scale of quantum resources is most likely to be achieved on NISQ devices in the near future.”
The team does point out in the paper that the quantum speedup of the algorithm is unclear due to the ambiguous convergence of QAOA, adding: “However, the idea of optimizing the “size-reduce” procedure in Babai’s algorithm through QAOA can be used as a subroutine in a large group of widely used lattice reduction algorithms. Further on, it can help to analyze the quantum-resistant cryptographic problems based on lattice.”
The researchers reported their findings in a paper uploaded to the ArXiv pre-print server. Papers on ArXiv are not officially peer-reviewed, so the team will likely submit the paper to a peer-reviewed journal for official results.
The team includes scientists from State Key Laboratory of Mathematical Engineering and Advanced Computing, Tsinghua University, Zhejiang University, Beijing Academy of Quantum Information Sciences, Information Engineering University and Frontier Science Center for Quantum Information.
If you found this article to be informative, you can explore more current quantum news here, exclusives, interviews, and podcasts.