
Quantum computing has the potential to revolutionize technology. While classical computing involves the use of bits (zeros and ones), to represent data, quantum computers benefit from the ability of “quantum bits” to be in a state of superposition. The quantum equivalent of “bits” are “qubits” and the phenomenon of Superposition allows these quantum entities to be in a state which is both zero and one at the same time. Stepping into the quantum world and getting acquainted with these non-intuitive quantum concepts can be tough.
We’ve made an attempt to introduce people to quantum circuits and thus create a base for entering the quantum world through our game. QLogic introduces the concepts of qubits and quantum gates to the player. It exposes them to exercises which involve the task of taking a system of qubits from one state to another by applying some common gates, such as the pauli-X gate (not-gate), the pauli-Z gate, the hadamard gate and their corresponding controlled gates.
Our aim is to subtly get the players familiar with the idea of qubits and quantum operations. We introduce concepts like superposition and entanglement as additional tips for our curious puzzlers. According to us, this makes the players question the rules of the quantum world and makes them eager to learn more about it. We have also planned to add more Informative features which would help them understand more about quantum computing.

The Math Behind QLogic
All the gate transformations performed in the game follow the rules of Vector Algebra to maintain consistency in programming all operations. We input the initial states as vectors and the gates are represented as matrices. The resultant system state is obtained from the matrix multiplication of the gate matrix and the state vector. Every time a gate is applied, our algorithm creates the matrix which is to be operated on the whole system of qubits, instead of just the qubit that the gate is applied on. This ensures that no matter how the system is entangled, the operation affects all correlated qubits. The resultant vector obtained is saved for further operations and is then converted into its binary equivalent to showcase the updated current state on the game screen.
We currently have 75 levels with up to 3-qubit systems. The levels have been created so as to cover all the different ways a qubit-system may transit. This maintains a variety in levels and also helps avoid repetition. The levels are designed so as to make the player optimize his/her moves according to the constraints: While some levels require you to get to the final state in minimum possible moves, others demand you to reach the result as quickly as possible in order to obtain 3 stars!
Game Modes
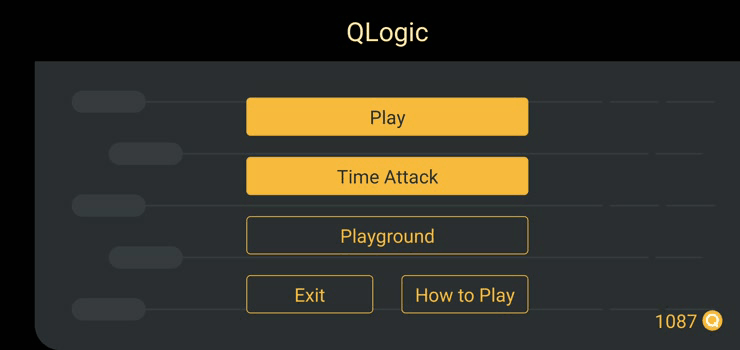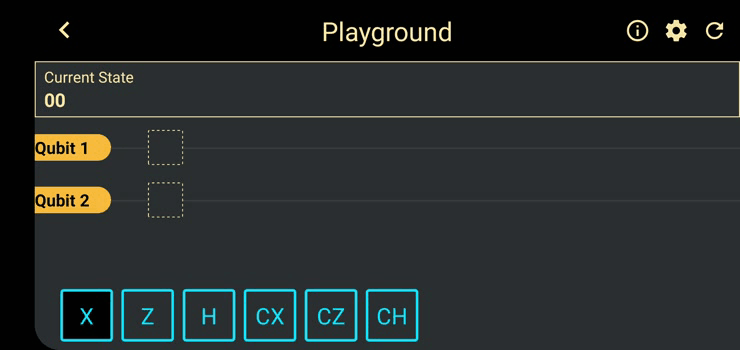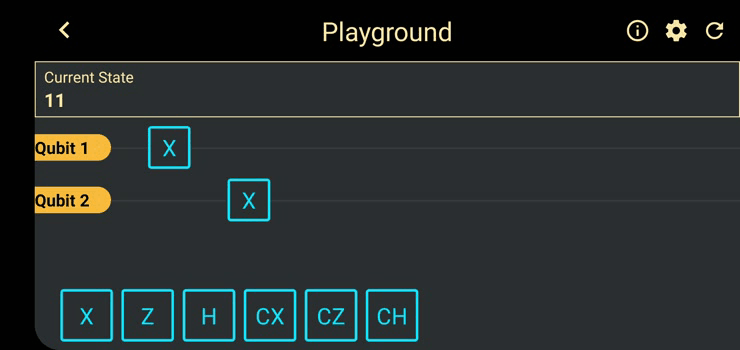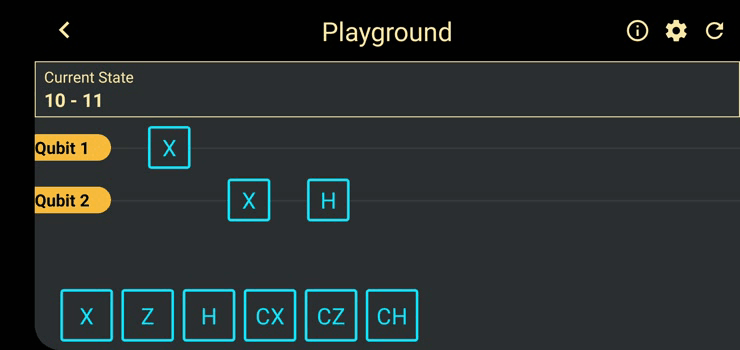
One interesting feature of QLogic is the Time Attack mode. Here, the players are supposed to create as many possible states as they can, from a given initial qubit state, in a certain time limit. One thinks of all the possible states a system can be in as he tries to reach the exhaustive set of states. This helps in giving him a complete overview of the quantum states. Players can play the time-attack mode for 2 and 3 qubit systems for a time limit of 60 and 90 seconds respectively and try to beat their personal highest scores (and will soon be able to compete against their friends on leaderboards).
QLogic also contains a ‘Playground’ feature which is meant to be an experimenting space. Players can think of an experiment and execute it here. The playground will soon have a ‘Normalization toggle’ and the option to input an initial state instead of the default |0> state.
Challenges
1) Normalization vs Gamification
Adding the eerie normalization factors, especially that leading from a Hadamard operation could make QLogic look less like a game and unnecessarily complicated for beginners. Consequently, we decided to ignore the amplitude part to focus more on making the levels look like puzzles which would teach the players to tackle multi-qubit systems.
2) Programming Gate operations
Gate operations had to be programmed in a way that it could handle superposition and entanglement well. Gates cannot be applied on individual qubits if the system is entangled. To avoid problems like these, we create a 2^n x 2^n dimensional matrix for the whole system of n qubits everytime a gate is applied on a qubit. This was especially challenging in case of controlled gates where the matrix depends on the relative indexes of control and the target qubit. Looking at the fundamentals of gate operations and vector algebra helped us design a generalised function for generating controlled-gate matrices.
3) Organizing Levels
Creating and ordering levels with gradually increasing difficulty and finding minimum possible moves was another excruciating task which required multiple checks. The levels were created considering different combinations of terms in case of multiple qubits. This ensured that the levels cover a wide variety of problems and are non-repetitive.
We are working on adding new features and modes which would make the game more informative and fun to play. Do try out the game on the android store and follow us on Instagram and Twitter for latest updates! If you have feedback/suggestions on how we can improve or make the game more interesting, you can get in touch directly with the QLogic team via our Telegram group.
For more market insights, check out our latest quantum computing news here.
















