“Think what we can do if we teach a quantum computer to do statistical mechanics,” posed Michael McGuigan, a computational scientist with the Computational Science Initiative at the U.S. Department of Energy’s Brookhaven National Laboratory.
At the time, McGuigan was reflecting on Ludwig Boltzmann and how the renowned physicist had to vigorously defend his theories of statistical mechanics. Boltzmann, who proffered his ideas about how atomic properties determine physical properties of matter in the late 19th century, had one extraordinarily huge hurdle: atoms were not even proven to exist at the time. Fatigue and discouragement stemming from his peers not accepting his views on atoms and physics forever haunted Boltzmann.
Today, Boltzmann’s factor, which calculates the probability that a system of particles can be found in a specific energy state relative to zero energy, is widely used in physics. For example, Boltzmann’s factor is used to perform calculations on the world’s largest supercomputers to study the behavior of atoms, molecules, and the quark “soup” discovered using facilities such as the Relativistic Heavy Ion Collider located at Brookhaven Lab and the Large Hadron Collider at CERN.
While it took a sea change to show Boltzmann was right, computer scientists now are at the precipice of a new computing wave, making the leap from supercomputers and bytes to quantum systems and quantum bits (or “qubits”). These quantum computers have the potential to unlock some of the most mysterious concepts in physics. And, oddly, these so-called mysteries may seem a bit familiar to many.

Time and Temperature Brought to You by…
Although most people are well acquainted with the notions of time and temperature and check on them several times a day, it turns out these basic concepts remain enigmatic in physics.
Boltzmann’s factor helps model temperature effects that can be used to predict and control atomic behavior and physical properties, and they work great on classical computers. However, on a quantum computer, the quantum logic gates used in the computation (akin to logic gates found in digital circuits) are represented by complex numbers, as opposed to Boltzmann’s factor, which by definition, is real.
This issue offered McGuigan and his student/coauthor Raffaele Miceli an interesting problem to tackle using a quantum computing testbed provided by way of Brookhaven Lab’s access agreement to IBM’s universal quantum computing systems, through the IBM Q Hub at Oak Ridge National Laboratory. The collaboration allows Brookhaven (among others in network) access to IBM’s commercial quantum systems, including 20- and 53-qubit systems for experiments.
“On a quantum computer, there is another way to simulate finite temperature called thermo field dynamics, which is able to compute quantities that are both time- and temperature-dependent,” McGuigan explained. “In this formalism, you construct a double of the system, called the thermo double, then proceed with the calculation on a quantum computer as the computation can be represented in terms of quantum logic gates with complex numbers.
“In the end, you can sum the double states and generate an effective Boltzmann’s factor for calculations at finite temperature,” he continued. “There also are certain advantages of the formalism. For example, you can study the effects of finite temperature and how the system evolves in real time as time and temperature are separated using this quantum algorithm. One disadvantage is that it requires twice as many qubits as a zero temperature calculation to handle the double states.”
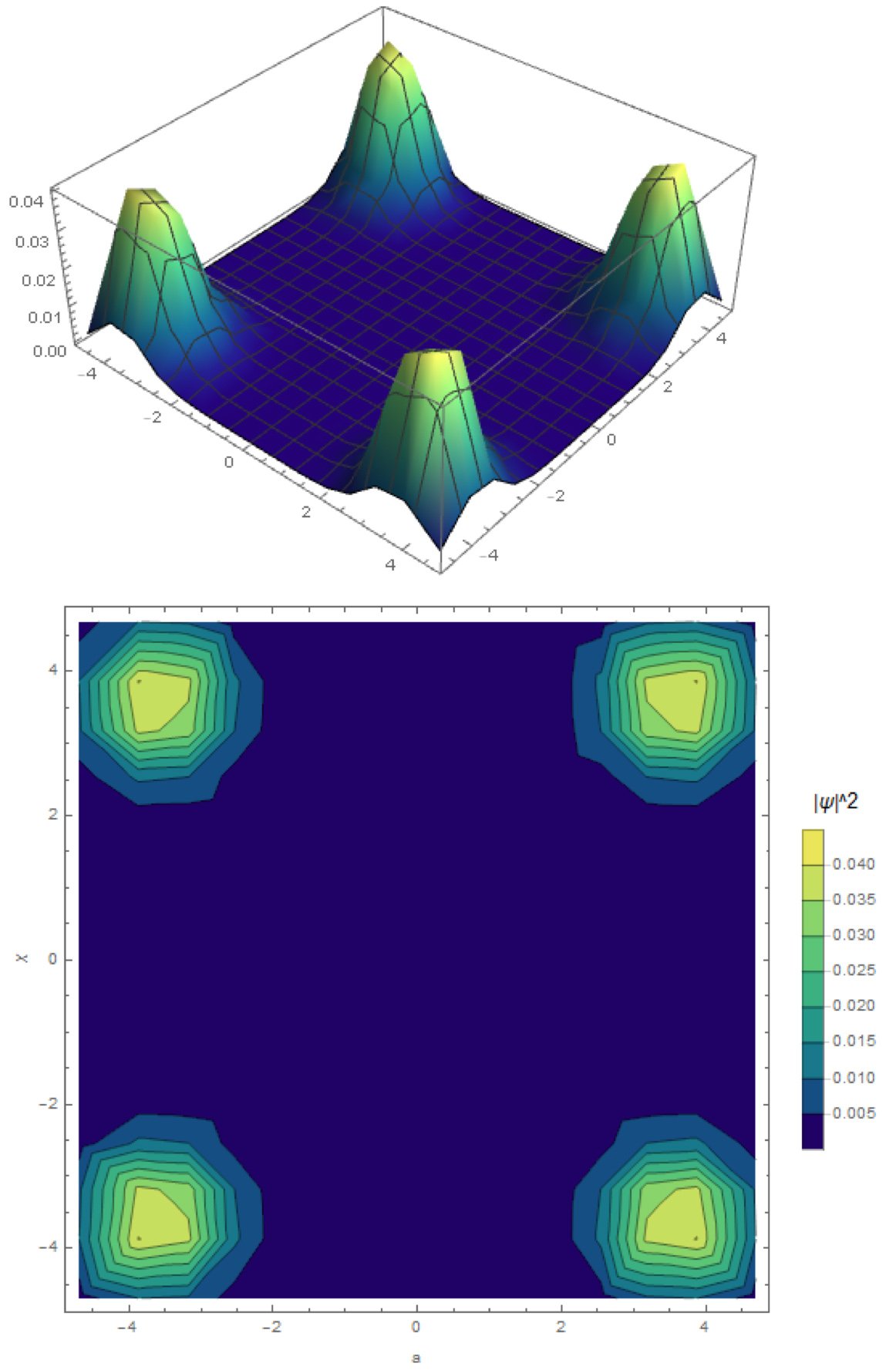
Miceli and McGuigan demonstrated how to implement the quantum algorithm for thermo field dynamics for finite temperature on a simple system involving a few particles and found perfect agreement with the classical computation.
Their work used resources from both classical and quantum computing. According to McGuigan, they used Qiskit open-source quantum computing software that allowed them to create their algorithm in the cloud. Qiskit then transpiled that code to pulses that communicate with a quantum computer in real time (in this case, an IBM Q device). Optimizers that run classical algorithms further enable the back and forth between the traditional and quantum systems.
“Our experiment shows quantum systems have an advantage of representing real-time calculations exactly rather than rotating from imaginary time to real time to find a result,” McGuigan explained. “It offers a truer picture of how a system evolves. We can map the problem to a quantum simulation that lets it evolve.”
Into the Cosmos
Quantum cosmology is another area where McGuigan anticipates that new quantum computing options will have profound impact. Despite the multitude of advances in understanding the universe made possible by modern supercomputers, some physical systems remain beyond their reach. The mathematical complexity, which usually includes accounting for full quantum gravity theory, is simply too great to obtain exact solutions. However, a true quantum computer, complete with the ability to exploit entanglement and superposition, would expand the options for new, more precise algorithms.
“Quantum systems can realize path integrals in real time, giving us access to large-scale simulations of the universe,” McGuigan said. “You can visualize the calculated wavefunction of the universe as it evolves forward without first formulating a full theory of quantum gravity.”
Again, using the Qiskit package and access to IBM Q hardware, McGuigan and his collaborator Charles Kocher, a student at Brown University, employed a mix of classical computational methods and VQE to run varied experiments, including one that examined systems with gravity coupled to a boson field called an inflaton, a hypothetical particle that plays an important role in modern cosmology. Their work showed the hybrid VQE yielded wavefunctions consistent with the Wheeler-Dewitt equation, which mathematically combines quantum mechanics with Albert Einstein’s theory of relativity.
Inspiration on an Expanding Scale
While early quantum experiments are leading to different perspectives of the basics behind physics, quantum computing is expected to contribute major advances toward solving longstanding problems impacting DOE’s missions. Among them, it can be a tool for unveiling new materials, solving energy challenges, or adding to fundamental understandings (like time and temperature) in high energy physics and cosmology. In turn, these changes could cascade into more readily recognizable areas.
For example, drug developers need more realized quantum mechanics to understand the structure of molecules. Quantum computers can enable discoveries by affording simulations of the full quantum mechanics that would provide a truly practical point of view.
“There seems to always be interest in the basics behind physics,” McGuigan said. “It has been of interest to the public for millennia. Right now, the combination of theoretical expertise and actual technology is converging with quantum computing. Yet, it still is a very human endeavor.”
For now, using near-term quantum computers to solve small thermo field problems or to take a new look at an old universe is inspiring researchers to scale up their algorithms as they do bigger things in science.
“We get emboldened to do different things. We all do,” McGuigan said. “Other groups around the world, such as the Perimeter Institute in Canada and Universiteit van Amsterdam in the Netherlands, are already extending the thermo field double quantum algorithm to even bigger systems. With the emergence of large near-term quantum computers of 50-100 qubits, the goal is to run finite temperature simulations on realistic systems involving many particles. It is exciting to have an actual quantum computer to test these ideas and problems that we once had no solutions for. Quantum mechanics with no tradeoffs—that is what science is all about.”
This research was supported by DOE’s Office of Science and the Supplemental Undergraduate Research Program (SURP) at Brookhaven Lab.
Provided by — Brookhaven National Laboratory. The lab is supported by the Office of Science of the U.S. Department of Energy.